9614. Coin change problem
You are working
as a cashier at a cheerful fair, and you have coins of different denominations.
An unlimited number of coins is available for each denomination, and the value
of each denomination is known. Determine the number of ways to pay a given amount
using the available coin denominations.
For example, if
you have 4 coin denominations with values 8, 3, 1, and 2, the amount 3 can be
paid in the following ways: {1, 1, 1}, {1, 2}, and {3}.
Input. The first line
contains two integers: the amount n (1 ≤ n ≤ 250) and the number of coin denominations m (1 ≤ m ≤ 50). The second line contains m integers ci (1 ≤ ci ≤ 50), representing the values of the coin denominations.
All ci values are distinct.
Output. Print the number
of ways to pay the amount n.
|
Sample
input 1 |
Sample
output 1 |
|
4 3 1 2 3 |
4 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
10 4 2 5 3 6 |
5 |
SOLUTION
dynamic programming
Algorithm analysis
Let f(k, n)
denote the number of ways to make the sum n using the first k denominations
of coins. This number is equal to the sum of two quantities:
·
the number of ways to make the sum n using the
first (k – 1) denominations (i.e., without using the k-th
denomination), and
·
the number of ways to make the sum (n – ak) using all k denominations.
Thus, we have
the following relationship:
f(k, n) = f(k – 1, n) + f(k, n – ak)
Initially, we
set f(0, 0) = 1, f(0, n) = 0 for n > 0.
Example
Let’s
consider the second example. Here, the sum n = 10 and there are k = 4 denominations.
The last denomination has a value of ak = 6. According to the relationship, we have:
f(4, 10) = f(3, 10) + f(4, 4)
The sum of 10 can be made
using the first three denominations {2, 5, 3} in 4 ways:
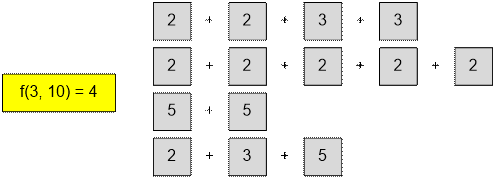
The sum of 4 can be made
using all four denominations {2, 5, 3, 6} in 1 way:
![]()
Algorithm realization
Declare the
arrays.
long long
dp[51][251];
int a[51];
The value
of f(k, n) will be stored in dp[k][n].
long long f(int k, int n)
{
if (k
== 0 && n == 0) return 1;
if (k
== 0 || n < 0) return 0;
if
(dp[k][n] != -1) return dp[k][n];
return
dp[k][n] = f(k - 1, n) + f(k, n - a[k]);
}
The main
part of the program. Read the input data.
memset(dp, -1, sizeof(dp));
scanf("%d %d",
&n, &m);
for (i = 1; i <= m; i++)
scanf("%d",
&a[i]);
Print the
required number of ways.
printf("%lld\n",
f(m, n));
Python realization
The value
of f(k, n) will be stored in dp[k][n].
def f(k, n):
if k == 0 and n == 0:
return 1
if k == 0 or n < 0:
return 0
if dp[k][n] != -1:
return dp[k][n]
dp[k][n] = f(k - 1, n) + f(k, n - a[k])
return dp[k][n]
The main
part of the program. Read the input data.
n, m = map(int, input().split())
a = [0] + list(map(int, input().split()))
dp = [[-1 for _ in range(n + 1)] for _ in range(m + 1)]
Print the
required number of ways.
print(f(m, n))